Overview

Graphs are powerful data structures used in programming to represent relationships and connections between entities. Understanding the different components of a graph is essential for working with graph-based algorithms and solving complex problems. Let’s explore the key components of a graph:

1. Nodes (Vertices): Nodes, also known as vertices, are the fundamental building blocks of a graph. They represent individual entities or elements within the graph. In real-world scenarios, nodes could represent people, locations, web pages, or any other entities you want to model and analyze. In programming, nodes are typically represented using unique identifiers or objects.
2. Edges: Edges connect pairs of nodes in a graph and represent the relationships or connections between them. An edge can be thought of as a link or a pathway between two nodes. Depending on the context, edges may be directed (pointing from one node to another) or undirected (bi-directional). They can also have weights or labels to represent additional information associated with the connection.
3. Weight: In some graphs, edges may have weights or values assigned to them. Weighted edges represent the strength, cost, distance, or any other attribute associated with the relationship between nodes. Weighted graphs are commonly used in algorithms like Dijkstra’s algorithm for finding the shortest path or in optimizing problems like network flows.
4. Directed and Undirected Graphs: Graphs can be categorized as either directed or undirected. In an undirected graph, edges have no specific direction and represent symmetric relationships. In a directed graph, each edge has a specific direction, indicating a one-way relationship from one node to another. Directed graphs are useful for modeling scenarios like network traffic or dependencies between tasks.
5. Cycles and Acyclic Graphs: A cycle in a graph is a path that starts and ends at the same node, passing through other nodes in between. A graph that contains cycles is called a cyclic graph, while a graph without any cycles is called an acyclic graph. Acyclic graphs are often used in topological sorting or representing hierarchical structures like organization charts.
6. Connectivity: Connectivity refers to the relationship between nodes in a graph. In a connected graph, there is a path between any two nodes. If a graph has multiple disconnected components, where some nodes are not reachable from others, it is considered a disconnected graph. Connectivity is crucial for analyzing the relationships and dependencies within a graph.

Working with graph-based algorithms and solving problems that involve relationships and connections between entities, requires a strong foundation in Graph Theory. By leveraging the power of graphs, developers can tackle challenges in areas such as social networks, routing, recommendation systems, and more.

What's the difference with a tree?

Property	Tree	Graph
Structure	A tree is a specific type of graph that has a hierarchical structure. It consists of nodes connected by edges, but the edges are directed and do not form cycles. Trees have a clear root node and a parent-child relationship between nodes.	A graph is a non-linear data structure consisting of nodes (vertices) connected by edges. The connections between nodes can be arbitrary, resulting in a more flexible and complex structure.
Connections	Trees have a hierarchical structure with a specific parent-child relationship. Each node (except the root) has a single parent node and zero or more child nodes. The edges in a tree are typically directed from parent to child, forming a directed acyclic graph (DAG).	Nodes can be connected to any other nodes through edges, allowing for arbitrary relationships and connections. Graphs can have both directed and undirected edges, and there can be multiple connections between nodes.
Complexity	Trees have a more organized and restricted structure, resulting in simpler algorithms and problems compared to general graphs. Many tree-based algorithms have lower time complexity as they exploit the hierarchical nature and balanced properties of trees.	Due to their flexible and arbitrary connections, graphs can represent complex relationships and dependencies. Graph algorithms and problems often have higher complexity compared to trees, as they involve traversing and analyzing potentially large and interconnected networks of nodes.
Connectivity	Always connected, meaning there is a path between any two nodes. Each node is reachable from the root node, forming a single connected component.	Graphs can have different connectivity properties, including connected graphs where there is a path between any pair of nodes, or disconnected graphs with multiple isolated components.

In Practice

Graphs: Graphs are widely used in various domains, such as social networks, routing algorithms, recommendation systems, network analysis, and graph databases. They excel at modeling complex relationships and dependencies.
Trees: Trees are commonly used in file systems, hierarchical data structures (e.g., XML, JSON), binary search trees, decision trees, syntax trees, and many more. They are suitable for representing hierarchical relationships and organizing data in a structured manner.

Practical Problem

The following problem was the May 20, 2023, daily challenge of LeetCode. It goes as follows:

You are given an array of variable pairs equations and an array of real numbers values, where equations[i] = [A_i, B_i] and values[i] represent the equation A_i / B_i = values[i]. Each A_i or B_i is a string that represents a single variable.

You are also given some queries, where queries[j] = [C_j, D_j] represents the jth query where you must find the answer for C_j / D_j = ?.

Return the answers to all queries. If a single answer cannot be determined, return -1.0.

Note: The input is always valid. You may assume that evaluating the queries will not result in division by zero and that there is no contradiction.
Example 1:

				
					Input:
    equations = [["a","b"],["b","c"]],
    values = [2.0,3.0],
    queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
Output: [6.00000, 0.50000, -1.00000, 1.00000, -1.00000]

How should one approach this problem? I will explain in a bit.

The Solution

Intuition

After thinking about the setting of the problem and playing with examples a bit, I found out that we need to somehow store a directed link between each coefficient, to be able to traverse between the links and reach from one coefficient to another, to calculate the queries.

For better demonstration, consider the inputs given in the example above. We can represent the relationships like this:

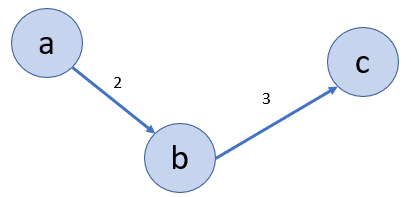
Approach

Foundation

We need two new structures:

Link: Holds a value and is directed, which means depending on the starting point and ending point, the value of the link will differ.
Node: Holds a name, and a list of all links connected to it.

				
					class Link:
    def __init__(self, val, start, end):
        self.val = val
        self.start = start
        self.end = end
        
class Node:
    def __init__(self, name: str):
        self.name = name
        self.links = set([Link(1.0, self, self)]) # => Read More
        self.prev_calcs = {name: 1.0} # => Check Note #1

If you don’t know what a DFS search is, check here.

Furthermore

Now we need to add a couple more properties to the above building blocks and improve the graph in this way:

Each node in the graph is also connected to itself with a value of 1.0.
Each pair of nodes should be traversable inversely as well.

This leads us to this final graph:

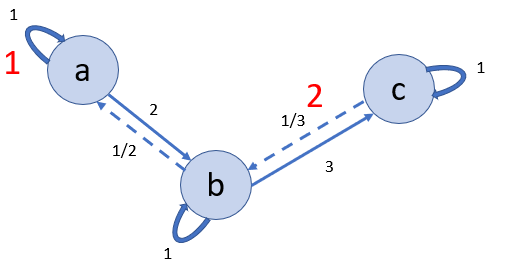
Complexity

Time Complexity
In the worst case, the amount of time it takes for each query would be equal to the number of equations, because, in the worst case, we may have to traverse the whole graph in order to reach the target.

O(len(equations)+len(queries)(len(equations))) = O(n(m+1))

Space complexity
Pretty hard to calculate, but it’s very inefficient sadly.

The Code

				
					class Link:
    def __init__(self, val, start, end):
        self.val = val
        self.start = start
        self.end = end
    
    # Optional method
    def __str__(self):
        return f"|-{self.start.name}--({self.val})--{self.end.name}->"


class Node:
    def __init__(self, name: str):
        self.name = name
        self.links = set([Link(1.0, self, self)])
        self.prev_calcs = {name: 1.0}
    
    # Optional method
    def to_json(self):
        return {"name": self.name, "links": list(map(str, self.links))}

    # Optional method
    def __eq__(self, other):
        if type(other) == str:
            return self.name == other
        elif type(other) == Node:
            return (self.name == other.name)
    
    # Establish a link between two Nodes
    def connect(self, other, val, is_mirror=False):
        self.links.add(Link(val, start=self, end=other))
        if not is_mirror:
            # `is_mirror` is added, to stop the infinite recursion
            other.connect(self, 1 / val, is_mirror=True)
        self.prev_calcs[other.name] = val
    
    # Calculate the total cost by recursive DFS traversal
    def calc_path(self, target_name: str, history=[]):
        res = None
        # For all links
        for link in self.links:
            # If the link.end is not checked yet
            if link.end.name not in history:
                # If the cost has been previously calculated
                if target_name in self.prev_calcs:
                    return self.prev_calcs[target_name]
                else:
                    # Start the search again, from the ending node
                    #  of the current link, and add the current node 
                    #  to history.
                    cost = link.end.calc_path(target_name, history + [self.name])
                    # If not found, keep searching
                    if cost == -1:
                        continue
                    # If found, return the total cost.
                    else:
                        # - `link.val` is the traversal cost
                        # - `cost` is the calculated cost from
                        #    the end node
                        res = link.val*cost
                        break
        # Return -1 if not found
        if not res:
            res = -1
        # Update the the `prev_calcs`
        else:
            self.prev_calcs[target_name] = res
        return res

class Solution:
    def calcEquation(self, equations: List[List[str]], values: List[float], queries: List[List[str]]) -> List[float]:
        nodes = {}
        # Create the nodes and link them
        for i, pair in enumerate(equations):
            try: node1 = nodes[pair[0]]
            except KeyError: node1 = Node(pair[0])
            try: node2 = nodes[pair[1]]
            except KeyError: node2 = Node(pair[1])
            node1.connect(node2, values[i])
            nodes[str(pair[0])] = node1
            nodes[str(pair[1])] = node2
        res = []
        # Iteratively calculate the path cost
        for q in queries:
            try: res.append(nodes[q[0]].calc_path(q[1]))
            except KeyError: res.append(-1)
        return res

Andrew

I’ve always been enthusiastic about software engineering so I started learning it myself. Today I’m a Self-Accomplished Senior Software Engineer and I have worked for many great companies and teams. I’m also great at learning languages and I love new adventures, be it new contacts, projects, or places.

Share this article:

Tagged Software Development

Graph Theory in Programming

Table of Contents